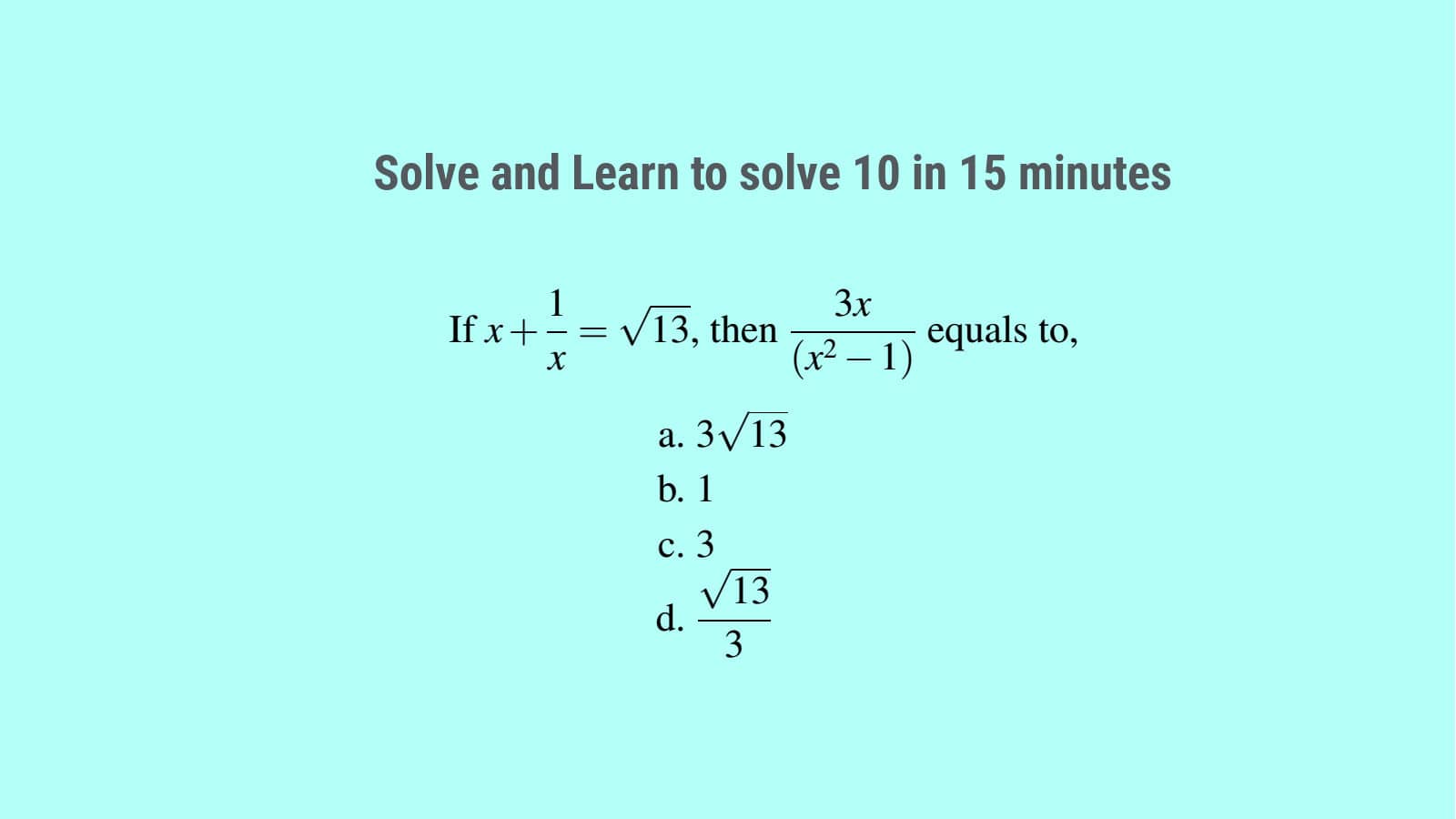
Surds and indices questions with solutions SSC CGL 93
Solve 10 surds and indices questions for SSC CGL set 93 in 15 minutes. Verify correctness from answers and finally learn how to solve from solutions.
The solved question set contains,
- Surds and indices questions for SSC CGL to be answered in 15 minutes (10 chosen questions)
- Answers to the questions, and,
- Detailed conceptual solutions to the questions.
For maximum gains, the test should be taken first, and then the solutions are to be read.
The answers and detailed solutions follow the questions.
First try to solve the questions yourself and then go through the solutions.
All problems are solved by specially quick methods based on discovered patterns.
10 surds and indices questions SSC CGL Set 93 - answering time 15 mins
Q1. Choose the incorrect relation from the following,
I. $\sqrt{6}+\sqrt{2}=\sqrt{5}+\sqrt{3}$
II. $\sqrt{6}+\sqrt{2} \lt \sqrt{5}+\sqrt{3}$
III. $\sqrt{6}+\sqrt{2} \gt \sqrt{5}+\sqrt{3}$
- II
- I and III
- I
- II and III
Q2. If $\displaystyle\frac{\sqrt{5+x}+\sqrt{5-x}}{\sqrt{5+x}-\sqrt{5-x}}=3$, then what is the value of $x$?
- $3$
- $4$
- $\displaystyle\frac{5}{2}$
- $\displaystyle\frac{25}{3}$
Q3. The value of $\displaystyle\frac{1}{\sqrt{7}-\sqrt{6}}-\displaystyle\frac{1}{\sqrt{6}-\sqrt{5}}+\displaystyle\frac{1}{\sqrt{5}-2}-\displaystyle\frac{1}{\sqrt{8}-\sqrt{7}}+\displaystyle\frac{1}{3-\sqrt{8}}$ is,
- $0$
- $5$
- $7$
- $1$
Q4. $55^3+17^3-72^3+201960$ is equal to,
- $-1$
- $17$
- $0$
- $1$
Q5. The value of $\displaystyle\frac{1}{\sqrt{(12-\sqrt{140})}}-\displaystyle\frac{1}{\sqrt{(8-\sqrt{60})}}-\displaystyle\frac{2}{\sqrt{10+\sqrt{84}}}$ is,
- $0$
- $1$
- $3$
- $2$
Q6. The value of $\sqrt{11-2\sqrt{30}}-\displaystyle\frac{1}{\sqrt{11-2\sqrt{30}}}$ is,
- $1+\sqrt{5}$
- $2\sqrt{5}$
- $2\sqrt{6}$
- $1+\sqrt{6}$
Q7. If $x=\sqrt{\displaystyle\frac{2+\sqrt{3}}{2-\sqrt{3}}}$, then what is the value of $x^2+x-9$?
- $3\sqrt{3}$
- $0$
- $3\sqrt{2}$
- $5\sqrt{3}$
Q8. If $P=7+4\sqrt{3}$ and $PQ=1$, then what is the value of $\displaystyle\frac{1}{P^2}+\displaystyle\frac{1}{Q^2}$?
- $182$
- $194$
- $196$
- $206$
Q9. If $\sqrt{3}=1.732$, then the value of $\displaystyle\frac{9+2\sqrt{3}}{\sqrt{3}}$ is,
- $7.169$
- $7.296$
- $7.196$
- $5.198$
Q10. If $x+\displaystyle\frac{1}{x}=\sqrt{13}$, then $\displaystyle\frac{3x}{(x^2-1)}$ equals to,
- $3\sqrt{13}$
- $1$
- $3$
- $\displaystyle\frac{\sqrt{13}}{3}$
Answers to the surds and indices questions SSC CGL set 93
Q1. Answer: Option b: I and III.
Q2. Answer: Option a: $3$.
Q3. Answer: Option b: $5$.
Q4. Answer: Option c: $0$.
Q5. Answer: Option a: $0$.
Q6. Answer: Option b: $2\sqrt{5}$.
Q7. Answer: Option d: $5\sqrt{3}$.
Q8. Answer: Option b: $194$.
Q9. Answer: Option c: $7.196$.
Q10. Answer: Option b: $1$.
Solution to the surds and indices questions SSC CGL Set 93 - answering time was 15 mins
Q1. Choose the incorrect relation from the following,
I. $\sqrt{6}+\sqrt{2}=\sqrt{5}+\sqrt{3}$
II. $\sqrt{6}+\sqrt{2} \lt \sqrt{5}+\sqrt{3}$
III. $\sqrt{6}+\sqrt{2} \gt \sqrt{5}+\sqrt{3}$
- II
- I and III
- I
- II and III
Solution 1: Quick solution by advanced surd expression comparison technique
You will find that no way can you compare $\sqrt{6}+\sqrt{2}$ and $\sqrt{5}+\sqrt{3}$ accurately (there is no place for approximation or guesswork here) unless you take special means to change the form of the two surd expressions. This is where the advanced never-failing technique of surd expression comparison comes in.
To start with, we will subtract $(\sqrt{5}+\sqrt{2})$ from both the given surd expressions without changing their greater lesser relationship, but transforming them to the desired form of,
$\sqrt{6}-\sqrt{5}$ and $\sqrt{3}-\sqrt{2}$.
This is the key pattern identification and corresponding action.
Observe that the difference between the integers under square root for both the expressions are equal. The surd expression comparison rule says,
If $(a-b)=(c-d)$ in two surd expressions, $\sqrt{a}-\sqrt{b}$ and $\sqrt{c}-\sqrt{d}$, then whichever of $a$ or $c$ is larger, corresponding surd expression will be the smaller one.
We will now show how the rule is true using our problem expressions.
Multiplying and dividing $\sqrt{6}-\sqrt{5}$, by $\sqrt{6}+\sqrt{5}$,
$\sqrt{6}-\sqrt{5}=\displaystyle\frac{1}{\sqrt{6}+\sqrt{5}}$.
Similarly,
$\sqrt{3}-\sqrt{2}=\displaystyle\frac{1}{\sqrt{3}+\sqrt{2}}$.
Now, $\sqrt{6}+\sqrt{5} \gt \sqrt{3}+\sqrt{2}$, as both integers under square root in the LHS are larger than those in the RHS.
Inverting the expressions inverts the comparison relation also. That is the inequality rule. So,
$\displaystyle\frac{1}{\sqrt{6}+\sqrt{5}} \lt \displaystyle\frac{1}{\sqrt{3}+\sqrt{2}}$.
Rationalize back to get our familiar expressions without changing the relationship,
$\sqrt{6}-\sqrt{5} \lt \sqrt{3}-\sqrt{2}$.
The result follows the rule we have described before.
Finally, following inequality rules again (which are very similar to equality rules) change sides of $\sqrt{5}$ and $\sqrt{2}$ with sign changed, without changing the relationship. Result is,
$\sqrt{6}+\sqrt{2} \lt \sqrt{5}+\sqrt{3}$.
I and III are the incorrect relations as II is the correct one.
Answer: Option b: I and III.
Key concepts used: Key pattern identification of transforming the two surd expressions to desired form -- Advanced surd expression comparison techniques -- Surd rationalization -- Inequality arithmetic -- Solving in mind.
If you know the technique that is based on basic concepts and also are clear about the inequality arithmetic, it should take very little time to find the answer.
Q2. If $\displaystyle\frac{\sqrt{5+x}+\sqrt{5-x}}{\sqrt{5+x}-\sqrt{5-x}}=3$, then what is the value of $x$?
- $3$
- $4$
- $\displaystyle\frac{5}{2}$
- $\displaystyle\frac{25}{3}$
Solution 2: Immediate solution by two-stage Componendo dividendo
LHS of the given equation is Componendo dividendo ready with both terms in numerator and denominator same except one differing in sign. So apply the three-step Componendo dividendo.
In first step add 1 to both sides, in second step subtract 1 from both sides and in third step take the ratio of the two. Result is,
$\displaystyle\frac{\sqrt{5+x}}{\sqrt{5-3}}=\frac{3+1}{3-1}=2$.
Get rid of the square roots by raising the simplified given equation to its square,
$\displaystyle\frac{5+x}{5-x}=4$.
The LHS is Componendo dividendo ready with both terms in numerator denominator same except one differing in sign.
So apply the three-step powerful Componendo dividendo again.
This time in first step subtract 1 from both sides, in second step add 1 to both sides and in third step take the ratio of the two. Immediate final result is,
$\displaystyle\frac{x}{5}=\frac{4-1}{4+1}=\frac{3}{5}$,
Or, $x=3$.
Answer: Option a: 3.
Key concepts used: Componendo dividendo in two stages -- Solving in mind.
Q3. The value of $\displaystyle\frac{1}{\sqrt{7}-\sqrt{6}}-\displaystyle\frac{1}{\sqrt{6}-\sqrt{5}}+\displaystyle\frac{1}{\sqrt{5}-2}-\displaystyle\frac{1}{\sqrt{8}-\sqrt{7}}+\displaystyle\frac{1}{3-\sqrt{8}}$ is,
- $0$
- $5$
- $7$
- $1$
Solution 3: Quick solution by Key pattern identification and rationalization
Identify the key pattern that in denominator of each term, the difference between the integers under square root is 1.
If you rationalize, for example the first one, $\displaystyle\frac{1}{\sqrt{7}-\sqrt{6}}$ by multiplying and dividing by $(\sqrt{7}+\sqrt{6})$, the denominator will turn to simply 1.
Rationalize then all the terms to simplify the target expression to,
$E=(\sqrt{7}+\sqrt{6})-(\sqrt{6}+\sqrt{5})+(\sqrt{5}+2)-(\sqrt{8}+\sqrt{7})+(3+\sqrt{8})$
$=3+2=5$.
Answer: Option b: $5$.
Key concepts used: Key pattern identification -- Surd rationalization -- Solving in mind.
Q4. $55^3+17^3-72^3+201960$ is equal to,
- $-1$
- $17$
- $0$
- $1$
Solution 4: Quick solution by Key pattern identification that $55+17=72$ and Compact form of cube of sum
Identify the key pattern that, the relation between the base integers of the first three cubes is,
$55+17=72$.
So, if you assume dummy variables, $a=55$ and $b=17$, the target expression is changed to,
$E=a^3+b^3-(a+b)^3+201960$
$=-3ab(a+b)+201960$, as $(a+b)^3=a^3+b^3+3ab(a+b)$
$=-3\times{55}\times{17}\times{72}+10\times{9}\times{2244}$
$=-10\times{9}\times{17}\times{11}\times{12}+10\times{9}\times{2244}$
$=-10\times{9}\times{2244}+10\times{9}\times{2244}$
$=0$.
Answer: Option c: $0$.
Key concepts used: Key pattern identification -- Compact form of cube of sum -- Simplifying calculation by use of factors -- Factor analysis.
Q5. The value of $\displaystyle\frac{1}{\sqrt{(12-\sqrt{140})}}-\displaystyle\frac{1}{\sqrt{(8-\sqrt{60})}}-\displaystyle\frac{2}{\sqrt{10+\sqrt{84}}}$ is,
- $0$
- $1$
- $3$
- $2$
Solution 5: Quick solution by double square root surd simplification of the three denominators
All three denominators are double square root surd expressions of simple kind so that the expressions under square root can easily be transformed into whole square expressions,
$12-\sqrt{140}=12-2\sqrt{35}=(\sqrt{7}-\sqrt{5})^2$,
$8-\sqrt{60}=8-2\sqrt{15}=(\sqrt{5}-\sqrt{3})^2$, and,
$10+\sqrt{84}=10+2\sqrt{21}=(\sqrt{7}+\sqrt{3})^2$.
Substituting, the target expression is simplified to,
$E=\displaystyle\frac{1}{\sqrt{(12-\sqrt{140})}}-\displaystyle\frac{1}{\sqrt{(8-\sqrt{60})}}-\displaystyle\frac{2}{\sqrt{10+\sqrt{84}}}$
$=\displaystyle\frac{1}{\sqrt{7}-\sqrt{5}}-\displaystyle\frac{1}{\sqrt{5}-\sqrt{3}}-\displaystyle\frac{2}{\sqrt{7}+\sqrt{3}}$.
Now rationalize the three denominators. First two denominators will be 2 and the third 4. The target expression is simplified further to,
$E=\displaystyle\frac{1}{2}\left[(\sqrt{7}+\sqrt{5})-(\sqrt{5}+\sqrt{3})-(\sqrt{7}-\sqrt{3})\right]$
$=0$
Answer: Option a: $0$.
Key concepts used: Double square root surd simplification -- Surd rationalization -- Solving in mind.
Q6. The value of $\sqrt{11-2\sqrt{30}}-\displaystyle\frac{1}{\sqrt{11-2\sqrt{30}}}$ is,
- $1+\sqrt{5}$
- $2\sqrt{5}$
- $2\sqrt{6}$
- $1+\sqrt{6}$
Solution 6: Quick solution by double square root surd simplification and surd rationalization
The surd expression $11+2\sqrt{30}$, being under square root is a double square root surd and must be expressed as a whole square of a sum of surd to get free of the outer square root.
This is easily possible by splitting the numeric term 11,
$11+2\sqrt{30}=(\sqrt{6})^2+2.\sqrt{6}.\sqrt{5}+(\sqrt{5})^2$
$=(\sqrt{6}+\sqrt{5})^2$.
By this result, the target expression is simplified to,
$E=\sqrt{11-2\sqrt{30}}-\displaystyle\frac{1}{\sqrt{11-2\sqrt{30}}}$
$=(\sqrt{6}+\sqrt{5})-\displaystyle\frac{1}{(\sqrt{6}+\sqrt{5})}$.
Rationalize the denominator of the second term by multiplying and dividing by $(\sqrt{6}-\sqrt{5})$.
Still more simplified result is,
$E=(\sqrt{6}+\sqrt{5})-(\sqrt{6}-\sqrt{5})=2\sqrt{5}$.
Answer: Option b: $2\sqrt{5}$.
Key concepts used: Double square root surd simplification -- Surd rationalization -- Solving in mind.
Q7. If $x=\sqrt{\displaystyle\frac{2+\sqrt{3}}{2-\sqrt{3}}}$, then what is the value of $x^2+x-9$?
- $3\sqrt{3}$
- $0$
- $3\sqrt{2}$
- $5\sqrt{3}$
Solution 7: Solve in only a few steps by key pattern identification and multiplying and dividing expression under square root of given equation RHS by $(2+\sqrt{3})$
Though this problem again belongs to the category of double square root surd, identify the key pattern to multiply and divide the RHS expression under square root by $(2+\sqrt{3})$. Denominator result is 1 and numerator, $(2+\sqrt{3})^2$.
The given equation is simplified to,
$x=2+\sqrt{3}$.
Substitute in simplified target expression,
$E=x^2+x-9=x(x+1)-9$
$=(2+\sqrt{3})(3+\sqrt{3})-9$
$=6+3+5\sqrt{3}-9=5\sqrt{3}$.
Answer: Option d: $5\sqrt{3}$.
Key concepts used: Key pattern identification -- Surd rationalization to get rid of double square root surd -- Surd arithmetic -- Solving in mind.
Q8. If $P=7+4\sqrt{3}$ and $PQ=1$, then what is the value of $\displaystyle\frac{1}{P^2}+\displaystyle\frac{1}{Q^2}$?
- $182$
- $194$
- $196$
- $206$
Solution 8: Quick solution by key pattern identification of simple values of $P^2+Q^2$
As $PQ=1$ and $P=7+4\sqrt{3}$,
$Q=\displaystyle\frac{1}{7+4\sqrt{3}}=7-4\sqrt{3}$, by rationalization.
The target expression evaluates to,
$\displaystyle\frac{1}{P^2}+\displaystyle\frac{1}{Q^2}$
$=\displaystyle\frac{P^2+Q^2}{P^2Q^2}$
$=(7+4\sqrt{3})^2+(7-4\sqrt{3})^2=2(49+48)=194$, the middle terms cancel out.
Answer: Option b: $194$.
Key concepts used: Key pattern identification -- Surd rationalization -- Sum of additive and subtractive squares -- Solving in mind.
Q9. If $\sqrt{3}=1.732$, then the value of $\displaystyle\frac{9+2\sqrt{3}}{\sqrt{3}}$ is,
- $7.169$
- $7.296$
- $7.196$
- $5.198$
Solution 9: Quick solution by key pattern identification and surd term factoring to simplify target expression reducing calculation
It is identified that if $\sqrt{3}$ is factored out from the numerator by surd term factoring, the target expression is greatly simplified because of denominator elimination,
$\displaystyle\frac{9+2\sqrt{3}}{\sqrt{3}}$
$=\displaystyle\frac{\sqrt{3}(3\sqrt{3}+2)}{\sqrt{3}}=3\sqrt{3}+2=5.196+2=7.196$.
Answer: Option c: $7.196$.
Key concepts used: Key pattern identification -- Surd term factoring to cancel out denominator and simplify the target expression greatly that needed little computation -- Solving in mind.
Q10. If $x+\displaystyle\frac{1}{x}=\sqrt{13}$, then $\displaystyle\frac{3x}{(x^2-1)}$ equals to,
- $3\sqrt{13}$
- $1$
- $3$
- $\displaystyle\frac{\sqrt{13}}{3}$
Solution 10: Quick solution by key pattern identification of subtractive sum of inverses in the denominator of the target and principle of interaction of inverses
Given is a sum of inverses and driven by this fact, the key pattern identified in the target expression is that dividing both numerator and denominator by $x$, a subtractive sum of inverses can be created in the denominator,
$\displaystyle\frac{3x}{(x^2-1)}$
$=\displaystyle\frac{3}{x-\displaystyle\frac{1}{x}}$.
Raise the given equation to its square,
$x^2+2+\displaystyle\frac{1}{x^2}=13$.
Subtract 4 from both sides,
$x^2-2+\displaystyle\frac{1}{x^2}=\left(x-\displaystyle\frac{1}{x}\right)^2=9$,
Or, $x-\displaystyle\frac{1}{x}=3$.
And target expression value,
$E=\displaystyle\frac{3}{3}=1$.
Answer: Option b: $1$.
Key concepts used: Target matching by creation of subtractive sum of inverses in target expression to match it with the given expression -- Evaluation of the subtractive sum of inverses by principle of interaction of inverses -- Solving in mind.
Note: While taking the square root, $\left(x-\displaystyle\frac{1}{x}\right)=-3$ is ignored in this case, as this value would have the answer as $-1$ that is not in the choices.
End note
Observe that, each of the problems could be quickly and cleanly solved in minimum number of steps using special key patterns and methods in each case.
This is the hallmark of quick problem solving:
- Concept based pattern and method formation, and,
- Identification of the key pattern and use of the method associated with it. Every special pattern has its own method, and not many such patterns are there.
Important is the concept based pattern identification and use of quick problem solving method.
Guided help on Fractions, Surds and Indices in Suresolv
To get the best results out of the extensive range of articles of tutorials, questions and solutions on fractions, surds and indices in Suresolv, follow the guide,
The guide list of articles includes ALL articles on Fractions, Surds and Indices and relevant topics in Suresolv and is up-to-date.