World's Hardest Easy Geometry Puzzle Solved with Techniques Explained Step by Step

World's hardest easy geometry problem step by step solution by increasing symmetry

World's hardest easy geometry problem is to be solved by elementary geometry only and that makes it hard.

Hint: Increase symmetry in the puzzle figure.

Often it is possible to easily solve hard geometry puzzles using advanced geometry concepts or even trigonometry concepts. Otherwise such puzzles cannot be solved. In the special case of this puzzle, it can be solved using elementary school geometry as well as more advanced concepts.

Allowing only elementary geometry makes it hard and at the same time challenges large number of general puzzle enthusiasts all over the world.

We'll simplify the problem step by step.

But you must make a good try before going through the solution. It will surely be fun.

The hardest easy geometry problem

In the figure, find $\angle x$.

There is no time limit for solving the puzzle.

Make your best try to solve it. It will be engaging and entertaining.

Solution to World's hardest easy geometry problem: Stage 1: Trial run and key pattern discovery

Let us put the required labels such as A, B, C and see the figure again.

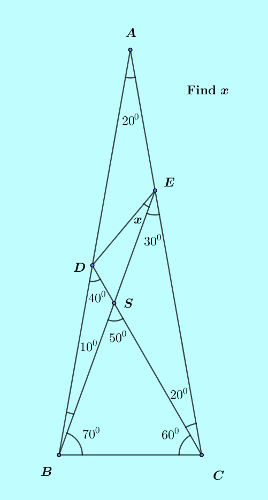
It is easy to evaluate many of the angle values quickly. Do that. We have also done it. This is trial run, always on the cards.

The angle values we get are,

$\angle BSC=\angle DSE=180^0-(60^0+70^0)=50^0$,

$\angle BSD=\angle CSE=180^0-50^0=130^0$,

$\angle BDC=180^0-(80^0+60^0)=40^0$,

$\angle BEC=180^0-(80^0+70^0)=30^0$.

Go ahead, jot down the angle values.

Finally this may not be used in the solution, but the good thing about this is—now you know how far you can go easily and meet the first bottleneck.

Till now we have used only one geometry concept,

Sum of three angles in a triangle is $180^0$.

But now we can discover the most important pattern till this point of time,

$\triangle ABC$ is isosceles, as $\angle ABC=70^0+10^0=60^0+20^0=80^0=\angle ACB$.

As a bonus we know the value of the $\angle BAC=180^0-2\times{80^0}=20^0$.

This is the first key pattern identification.

Still the values of three key angles, $\angle ADE$, $\angle SDE$, $\angle DEA$ elude us.

This is natural as the puzzle is hard.

In such a puzzle, unless we introduce new elements in the given puzzle figure, the deadlock cannot be broken.

At the end of this first stage of trial run, we discover the second key pattern,

$\triangle ADC$ is also isosceles as $\angle CAD=\angle DCA=20^0$.

Solution to World's hardest easy geometry problem: Stage 2: Identification of most promising concept for solution

Now that we have experienced the difficulty in solving the puzzle, we would naturally ask ourselves,

What is the main reason behind this difficulty?

Answer lies in asymmetry of the target triangle.

The $\angle x$ is formed as a part of $\triangle DES$ that lies inside the larger $\triangle ABC$ ASYMMETRICALLY, and that has created all the difficulties. We are not able to evaluate the desired elements of this asymmetric triangle from other known angle values in the larger triangle.

A general truth in solving geometry puzzles is,

Unless we can use the concepts that are based on symmetric or equivalent shapes, we won't be able to solve a hard geometry puzzle. This is what we call principle of symmetry in shapes.

Why?

The reason lies behind the characteristics of the geometry concepts that we can use as problem solving resources.

In this case of a puzzle involving triangles, the concepts that we can possibly use for solving the problem are,

1. Properties of isosceles triangles: We have already discovered not just one, but two such triangles, and both are symmetric shapes.
2. Properties of equilateral triangles: We don't have yet an equilateral triangle. Because of higher degree of symmetry of an equilateral triangle compared to an isosceles triangle, it would have provided us with more problem solving resources if we could have identified (or introduced) a suitable equilateral triangle in the problem figure.
3. Properties of similar triangles: We don't have any pair of similar triangles yet, but let us know for sure that this pattern in a geometric figure provides us with rich problem solving resources.

There are other more advanced concept based properties of triangles, but first,

We must use the most basic concept based properties in a problem domain. In most cases that would give us the simplest and quickest solution.

Identification of most promising concept based pattern as resource for solving this problem

Based on all these analysis, we have finally made up our mind about the most important problem solving resource to target,

As the problematic angle location is asymmetric, the most promising concept based pattern should be a pair of similar triangles.

Basis of this conclusion and deciding on more specific action to be taken

Finding a second suitable triangle similar to $\triangle ADE$ or $\triangle DSE$ being not easily visible, the most promising action decided is to find a triangle that is similar to $\triangle BAE$ that contains target $\angle x$.

If we attempt this, all three angles of $\triangle BAE$ being known and $\angle A$ being twice the $\angle ABE$, the big advantages would be,

1. It should be easy to create this new triangle similar to $\triangle BAE$, and also,
2. If we are successful, we should get valuable information on the angles and sides of the second similar triangle leading to the target angle value.

How to create such a new similar triangle?

That is also easy.

But let us first see the more complete diagram.

To create a second triangle similar to $\triangle BAE$,

Just draw an angle bisector AF of $\angle BAC$ to make $\angle BAF=\angle ABE=10^0$.

Not surprisingly, AF intersects CD at F, creating an equilateral $\triangle BFC$ and $\angle ABF$ becomes equal to $20^0$, which is the value of $\angle BAE$.

With $\angle ABE=\angle BAF=10^0$, all three corresponding pairs of angles of two triangles $\triangle BAE$ and $\triangle ABF$ are equal and the triangles turn out to be similar as we wanted. As a bonus, the triangles turn out to be congruent because side AB is common to both triangles.

Essentially, we have balanced out the asymmetry by introducing necessary and additional symmetry. This is asymmetry balancing technique that seems to be a quite in the clouds concept.

Why does an angle bisector create so much symmetry and new problem solving resources in this case?

This is because, in an isosceles triangle with sides adjacent to the apex angle equal, an angle bisector of the apex angle divides the triangle into two mirror images of half triangles that are both right triangles so that the angle bisector also bisects the base.

Natural outcome because of the symmetry introduced by the angle bisector AF will be creation of an equilateral triangle $\triangle BFC$,

$\angle CBF=\angle BCF=\angle BFC=60^0$.

As a byproduct, $\angle EBF$ turns out to be $10^0$ reducing $\angle CBE$ by $10^0$ from $70^0$ to $60^0$. 

So BE becomes the angle bisector of $\angle ABF$ just as AF is the angle bisector of $\angle BAE$.

All these favorable results could happen simply because $\triangle ABC$ is isosceles as well as the the way BE makes an angle of $70^0$ and CD makes an angle of $60^0$ with the same base BC.

All in all, this is the most important new set of elements we have introduced in the problem figure.

Okay, all these are just analysis of the internal anatomy of the geometry problem. But the immediate question is,

What should we do with this increased symmetry?

As it is easily visible now, let us increase the amount of symmetry further by identifying a second equilateral $\triangle DFG$. This should be helpful as we would be moving towards the problematic zone. This is the always effective abstract technique of increasing symmetry.

At this point, a wealth of problem solving resources in the form of a second equilateral triangle and a pair of similar triangles are available. Though lightly hidden, the path to the solution is clearly visible.

Final steps to the Solution to World's hardest easy geometry problem

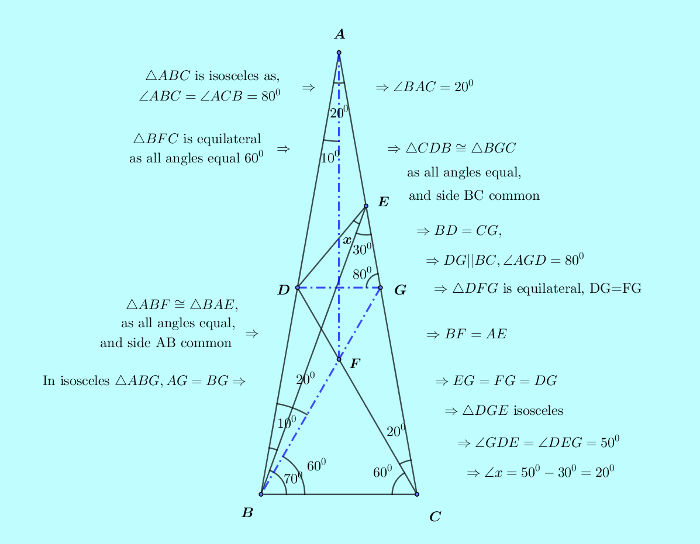
Let us assert the steps to the solution. We'll collect all new conclusions from starting point together to present the whole picture.

$\triangle ABC$ is isosceles as $\angle ABC=\angle ACB=80^0$.

$\triangle BFC$ is equilateral as all angles are equal to $60^0$.

We will now establish $DG||BC$.

$\triangle CDB \cong \triangle BGC$ as all angles are equal with side BC common,

$\Rightarrow BD=CG$,

$\Rightarrow$ due to similarity of $\triangle ABC$ and $\triangle ADG$, $DG||BC$.

$\Rightarrow \triangle DFG$ is equilateral,

$\Rightarrow DG=FG$, $\angle AGD=80^0$.

Again as all corresponding pairs angles are equal with side BC common,

$\triangle ABF \cong \triangle BAE$,

$\Rightarrow BF=AE$,

So, in isosceles $\triangle ABG$,

$AG=BG$,

Or, $AE+EG=BF+FG$,

Or, $EG=FG=DG$, as in equilateral $\triangle DFG$ we already had, $DG=FG$.

So, in $\triangle DGE$, as $EG=DG$, it is isosceles with its two base angles equal to each other.

With apex $\angle EGD=\angle AGD=80^0$ in equilateral $\triangle DGE$,

$\angle DEG=\displaystyle\frac{180^0-80^0}{2}=50^0$.

And finally,

$x=50^0-\angle BEC=50^0-30^0=20^0$.

That is the answer, $\angle x=20^0$.

The solution schematic is shown below,

There are more ways to solve this puzzle and this solution is among the simplest.

Overall, this puzzle problem should be considered as a source of puzzle solving excitement as well as a valuable piece of geometry problem rich with teaching potential for young school students anywhere.

Recommendation

This is a rich problem to solve.

Try out on your own for new solutions.

---

Know how to solve difficult problems easily without wasting time on random attempts

Our ebook on puzzle solutions by innovative methods will show you just that.

Puzzles for Adults: 50 Brain Teasers with Step-by-Step Solutions: Boost Your Power of Problem Solving

(BUY from Apple books, Barnes & Noble, Rokuten Kobo, Vivlio, Angus & Robertson, Tolino, PayHip and others)

BUY the eBook Amazon Kindle version here, from Google Play here and Paperback here.

---

Puzzles you may enjoy

Easy to hard brain teasers with systematic solutions

Challenging brain teasers with solutions: Long list.

This will always be the most up-to-date full list with the brain teasers classified into categories that can be browsed separately.

You may also click on the category term link below to enjoy the brain teasers that are classified in the present category.

For example, if the category term link shown below is "Riddle", click on it to go through all the Riddles.

---