
How Secant of a Circle is related to tangent segment to the Circle
Secant of a circle relation: Square of a tangent segment from an external point equals product of two segments of a secant of a circle through the point.
Content sections are,
- Secant of a Circle and tangent segment relation: Concept and proof of relation.
- External angle equality property of a chord in a circle: concept and proof in brief.
- Arc angle subtending relation: Concept and proof in brief.
To understand and prove the Secant of a circle segment relation, External angle equality property is to be used which in turn uses the Arc angle subtending relation.
Though we'll present the Secant of a circle relation first, you may jump to any of the other two concept sections by clicking on the internal links provided and return by browser back button click.
For example click on this link of Arc angle subtending relation to jump to the corresponding third section. Return to this point again by clicking on browser back button.
Secant of a Circle and Tangent segment relation
In short we call this relation as secant of a circle segment relation. The following graphic will be used for stating and proving the important property.
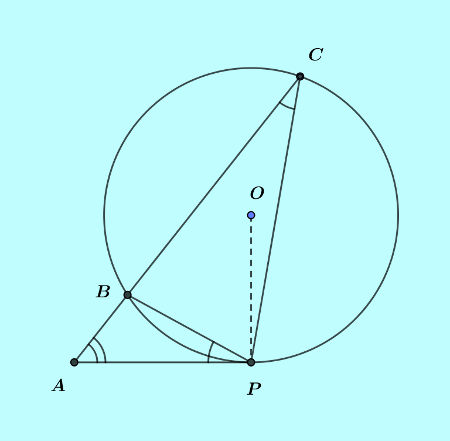
The secant of a circle segment property states,
The square of a tangent segment to a circle from an external point will be equal to the product of the two segments of a secant of the circle through the point.
In the graphic, AP is the tangent segment of the circle from external point A and ABC is the secant of the circle through point A. The circle segments the secant into AB and BC.
By the secant of a circle segment relation,
$AP^2=AB.AC$.
Let us see how this property comes true.
Observe that by external angle property of a chord, $\angle APB=\angle ACP$ in two triangles $\triangle ABP$ and $\triangle ACP$.
(To refresh the concept on External angle equality property of a chord in a circle click on the above link and return by clicking on browser back button)
With $\angle A$ common, the third pair of angles are equal,
$\angle ABP=\angle APC$.
With all three pairs of angles equal, by A-A-A property, the two triangles are similar.
In a pair of similar triangles, ratio of corresponding pairs of sides are equal. So by this property,
$\displaystyle\frac{AP}{AC}=\frac{AB}{AP}$,
Or, $AP^2=AB.AC$.
Thus it is proved that square of tangent segment to a circle from an external equals the product of two segmants made by the secant of the circle through the point.
In the first ratio of LHS, AP in numerator and AC in denominator are opposite to equal angles $\angle ABP$ in $\triangle ABP$ and $\angle APC$ in $\triangle APC$ respectively.
Similarly, in the second RHS ratio, AB in numerator and AP in denominator are opposite to equal angles $\angle APB$ in $\triangle ABP$ and $\angle ACP$ in $\triangle APC$ respectively.
These form the corresponding pairs of sides.
Observe how the proving of the secant of a circle relation needed the understanding of external angle equality property of a chord in a circle.
External angle equality property of a chord and its short proof
The following graphic will be used for stating and proving the concept.

SA is the tangent to the circle at point A where it is perpendicular to the radius OA.
The $\angle SAB$ held by the chord BA at tangent point A with the tangent segment SA is called the external angle of the chord.
The external angle property of a chord states,
The external angle of a chord will be equal to the angle held by the chord at any point on the alternate segment of the periphery. To be specific, $\angle SAB=\angle APB=\theta$.
Let us understand how this result comes true.
Let, $\angle SAB=\theta$.
As radius OA is perpendicular to SA at tangent point A,
$\angle SAB+\angle BAO=90^0$,
Or, $\angle BAO=\angle ABO=90^0-\theta$, as radii $OA=OB$ in isosceles $\triangle OAB$.
So in $\triangle OAB$,
$\angle AOB=180^0-2[90^0-\theta]=2\theta$.
This being the angle held by the chord AB at the centre, by arc angle subtending property, it is double the angle held by the same chord AB at the point P or Q on the alternate segment of the corresponding arc AB on the periphery.
So, $\angle SAB=\angle APB=\angle AQB=\theta$.
This is how secant of a circle and tangent segment relation needs understanding of external angle equality property of a chord which in turn uses the arc angle subtending relation in a chain of three important concepts on a circle.
Arc angle subtending concept in a Circle and its short proof
We'll use the following graphic for stating and explaining the concept.

The important arc angle subtending concept in a circle states,
An arc segment in a circle subtends the same angle at every point on the alternate arc segment of the circle, and at the centre of the circle, the arc subtends an angle double the angle it subtends on the alternate segment of the periphery.
Let us see how this property comes to be true.
The small segment of the arc AB subtends an angle $\angle \theta$ at P on the alternate segment of the periphery.
Being the radii, $AO=PO$ and in isosceles $\triangle AOP$, the two base angles,
$\angle PAO=\angle APO=x$, say.
Similarly, in isosceles $\triangle BOP$, the two base angles,
$\angle PBO=\angle BPO=y$, say.
So, $\angle APB = x+y=\theta$, say.
Now in $\triangle AOB$,
$\angle AOB=180^0-(\angle OAB+\angle OBA)$.
In larger $\triangle PAB$,
$(\angle OAB+\angle OBA)=180^0-2(x+y)$.
So,
$\angle AOB=180^0-[180^0-2(x+y)]=2(x+y)=2\theta$.
The same is true for $\angle AQB$ subtended by the arc AB at a second point Q (and any other point) on the alternate arc segment of the periphery.
At all points on the alternate arc segment of the periphery, the arc AB holds the same angle $\theta$ that is half the angle it holds at the centre.
Guided help on Geometry in Suresolv
To get the best results out of the extensive range of articles of tutorials, questions and solutions on Geometry in Suresolv, follow the guide,
The guide list of articles includes ALL articles on Geometry and relevant topics in Suresolv and is up-to-date.