
Quick solutions to Trigonometry Questions for SSC CGL Tier 2 Set 18
Trigonometry Identity Questions Solutions for SSC CGL tier 2 Set 18 explains clearly how the 10 difficult trigonometry questions can be solved in 12 mins.
For best results take the test first at,
18th SSC CGL Tier II level question set and 4th on Trigonometry.
Solution to 10 Trigonometry questions for SSC CGL Tier 2 Set 18 - testing time was 12 mins
Problem 1.
The value of
$\displaystyle\frac{4\cos(90^0- \theta)\sin^3(90^0+\theta)-4\sin(90^0+\theta)\cos^3(90^0-\theta)}{\cos\left(\displaystyle\frac{180^0+8\theta}{2}\right)}$ is,
- $0$
- $-1$
- $1$
- $2$
Solution 1. Problem analysis: Compound angle, Complementary angle and Supplementary angle trigonometric functions: Multiple angle Trigonometric functions
First the compound angle, complementary angle and supplementary angle trigonometric functions are to be converted and then multiple angle trigonometric relations are to be applied.
The following section covers these concepts that would be used throughout the solutions. If you are aware of the concepts, you may skip it.
Compound angle trigonometric functions on $(\alpha+\beta)$
When the angle of a trigonometric function is a sum of two angles (additive or subtractive), we have a compound angle trigonometric function. For dealing with such a function in simplifications, it needs to be expanded in terms of trigonometric functions on individual elementary angles.
Two main additive compound angle trigonometric relations you need to remember are,
$\sin(\alpha+\beta)=\sin \alpha\cos \beta+\cos \alpha\sin \beta$, and
$\cos(\alpha+\beta)=\cos \alpha\cos \beta-\sin \alpha\sin \beta$.
From these two basic relations we can easily deduce the other two subtractive angle relations,
$\sin(\alpha-\beta)=\sin \alpha\cos \beta-\cos \alpha\sin \beta$, and
$\cos(\alpha-\beta)=\cos \alpha\cos \beta+\sin \alpha\sin \beta$.
This happens because,
$\sin (-\theta)=-\sin \theta$, and
$\cos (-\theta)=\cos \theta$.
These two are negative angle reflexive trigonometric relations.
Complementary angle trigonometric functions on $(90^0-\theta)$
By definition,
Two angles are complementary if sum of the two is $90^0$.
The complementary angle trigonometric relations are,
$\sin(90^0-\theta)=\cos \theta$.
$\cos (90^0-\theta)=\sin \theta$.
And so,
$\tan (90^0-\theta)=\text{cot }\theta$, and
$\text{cot } (90^0-\theta)=\tan \theta$.
$\sec (90^0-\theta)=\text{cosec }\theta$.
$\text{cosec }(90^0-\theta)=\sec \theta$.
In all these relations $\theta$ is acute, and resultant angle is in first quadrant.
These are easy to remember. Only two things you need to keep in mind,
- First: the broad concept of trigonometric function pairs: $\sin$ paired with $\cos$, $\text{cosec}$ paired with $\sec$ and $\tan$ paired with $\text{cot}$. These pairings are for determining complementary angle $(90^0-\theta)$, compound angle $(90^0+\theta)$ and supplementary angle $(\pi-\theta)$ transformations from one function of a pair to the other function of the same pair with only $\theta$ as the angle.
- Second: a function on $90^0$ minus an acute angle $\theta$ will always be equal to its paired function on just $\theta$.
Compound angle trigonometric relations on $(90^0+\theta)$
The compound angle trigonometric function relations with angles $90^0+\theta$ are,
$\sin (90^0+\theta)=\cos \theta$, and
$\cos (90^0+\theta)=-\sin \theta$.
The function nature reverses from $\sin$ to $\cos$ and vice versa with the only other point to remember—for $\cos$ sign becomes negative after reversal to $\sin$.
The other four relations on $\tan$, $\text{cot}$, $\text{cosec}$ and $\sec$ can easily be deduced from these two.
Here also $\theta$ is assumed to be an acute angle so that the resultant angle is in second quadrant.
Supplementary angle trigonometric relations
By definition,
Two angles are supplementary to each other if sum of the two is $180^0$ or $\pi$.
The relations for $\sin(\pi-\theta)$ is,
$\sin(\pi-\theta)=\sin \theta$.
Mechanism:
$\sin(\pi-\theta)=\sin \pi\cos \theta-\cos \pi\sin \theta$, from compound angle expansion
$=\sin \theta$, as $\sin \pi=0$, and $\cos \pi=-1$.
The relation for $\cos(\pi-\theta)$ is,
$\cos(\pi -\theta)=-\cos \theta$.
Mechanism:
$\cos(\pi-\theta)=\cos \pi\cos \theta+\sin \pi\sin \theta$
$=-\cos \theta$.
From these two, the other four function relations can easily be derived.
Multiple submultiple angle trigonometric functions, $2\alpha$ and $\displaystyle\frac{\alpha}{2}$
If $\alpha=\beta$ we get a multiple angle. The frequently used two relations are,
$\sin 2\alpha=2\sin \alpha\cos \alpha$, and
$\cos 2\alpha=cos^2 \alpha -\sin^2 \alpha$.
Deducing submultiple angle relations from multiple angle relations by suitable assumptions is straightforward.
Two important derived relations are,
$\sin \alpha +\sin \beta=2\sin\left(\displaystyle\frac{\alpha+\beta}{2}\right)\cos\left(\displaystyle\frac{\alpha-\beta}{2}\right)$, and
$\cos \alpha +\cos \beta=2\cos\left(\displaystyle\frac{\alpha+\beta}{2}\right)\cos\left(\displaystyle\frac{\alpha-\beta}{2}\right)$.
These are derived by assuming $p=\displaystyle\frac{\alpha+\beta}{2}$ and $q=\displaystyle\frac{\alpha-\beta}{2}$ so that $(p+q)=\alpha$ and $(p-q)=\beta$.
Thus,
$\sin \alpha=\sin(p+q)$, and $\sin \beta=\sin(p-q)$. When you expand the two and sum up, the two terms, $\cos q\sin p$ are eliminated leaving $2\sin p\cos q$.
This is why,
$\sin(p+q)+\sin(p-q)=2\sin p\cos q$,
Or, $\sin \alpha+\sin \beta=2\sin\left(\displaystyle\frac{\alpha+\beta}{2}\right)\cos\left(\displaystyle\frac{\alpha-\beta}{2}\right)$.
In the same way you can derive on the fly the relations, $(\cos \alpha +\cos \beta)$, $(\sin \alpha-\sin \beta)$, and $(\cos \alpha-\cos \beta)$.
Note: All the above special trigonometric functions relations can be derived from basically the first two general compound angle expanded relations on $\sin(\alpha+\beta)$ and $\cos(\alpha+\beta)$.
You may get a feel of most of the relations from the following graphic of $\sin$-$\cos$ curve.
Understanding compound angle trigonometric relation variations from $\sin-\cos$ curves
From the following superimposed $\sin-\cos$ curve you may realize why the above relations are true.
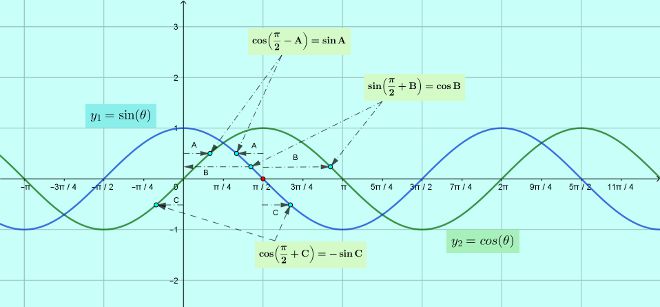
Solution 1: Converting compound, complementary and supplementary angle functions to elementary angle functions
Using the above relations, at the first step we will eliminate the compound $(90^0+\theta)$, complementary and supplementary angles and then use the multiple angle relation for $sin$,
$\displaystyle\frac{4\cos(90^0- \theta)\sin^3(90^0+\theta)-4\sin(90^0+\theta)\cos^3(90^0-\theta)}{\cos\left(\displaystyle\frac{180^0+8\theta}{2}\right)}$
$=\displaystyle\frac{4\sin\theta\cos^3\theta-4\cos\theta\sin^3\theta}{\cos(90^0+4\theta)}$
$=\displaystyle\frac{4\sin \theta\cos \theta(\cos^2 \theta- \sin^2 \theta)}{-\sin 4\theta}$
$=\displaystyle\frac{2\sin 2\theta\cos 2\theta}{-2\sin 2\theta\cos 2\theta}$, as $2\sin \theta\cos \theta=\sin 2\theta$, and $\cos^2 \theta-\sin^2 \theta=\cos 2\theta$,
$=-1$.
Answer: Option b: $-1$.
Key concepts and techniques used: Compound angle trigonometric function relations on $(90^0+\theta)$ -- Negative angle trigonometric function relations -- Complementary angle trigonometric function relations -- Supplementary angle trigonometric function relations -- Multiple angle trigonometric function relations.
Though the problem looked difficult, the solution steps could be carried out in mind.
Problem 2.
If $\sec \theta(\cos \theta+\sin \theta)=\sqrt{2}$ then the value of $\displaystyle\frac{2\sin \theta}{\cos \theta -\sin \theta}$ is equal to,
- $\sqrt{2}$
- $\displaystyle\frac{1}{\sqrt{2}}$
- $3\sqrt{2}$
- $\displaystyle\frac{3}{\sqrt{2}}$
Solution 2. Problem analysis and input transformation suitable for target expression simplification
From the given equation it is easy to evaluate the value of $\tan \theta$,
$\sec \theta(\cos \theta+\sin \theta)=\sqrt{2}$,
Or, $1 +\tan \theta=\sqrt{2}$
Or, $\tan \theta=\sqrt{2}-1$.
As the target expression is in $\sin$ and $\cos$ we can easily convert the expression wholly in terms of $\tan \theta$ and then substitute the value of $\tan \theta$,
$\displaystyle\frac{2\sin \theta}{\cos \theta -\sin \theta}$
$=\displaystyle\frac{2\tan \theta}{1-\tan \theta}$, dividing both numerator and denominator by $\cos\theta$,
$=\displaystyle\frac{2(\sqrt{2}-1)}{2-\sqrt{2}}$
$=\displaystyle\frac{2(\sqrt{2}-1)}{\sqrt{2}(\sqrt{2}-1)}$
$=\sqrt{2}$.
This is target driven input transformation. Both the given expression and the target expression are changed together so that the changed given expression can be used in the changed target expression in the best possible manner.
Answer: Option a: $\sqrt{2}$.
The key pattern identified is easy evaluation of $\tan \theta$ and possibility of transforming the target expression in terms of $\tan \theta$.
Key concepts and techniques used: Useful pattern identification and exploitation -- Basic trigonometry concepts -- Target driven input transformation -- Surd factoring -- Solving in mind.
All steps could easily be done in mind.
Problem 3.
The value of $\displaystyle\frac{(\sin x+\sin y)(\sin x - \sin y)}{(\cos x+\cos y)(\cos y - \cos x)}$ is,
- $0$
- $2$
- $1$
- $-1$
Solution 3. Problem analysis and solving
The opportunity of simplifying both numerator and denominator to two term expressions using algebraic relation, $(a+b)(a-b)=a^2-b^2$ is exploited first,
$\displaystyle\frac{(\sin x+\sin y)(\sin x - \sin y)}{(\cos x+\cos y)(\cos y - \cos x)}$
$=\displaystyle\frac{\sin^2 x-\sin^2 y}{\cos^2 y -\cos^2 x}$
$=\displaystyle\frac{\cos^2 y-\cos^2 x}{\cos^2 y -\cos^2 x}$
$=1$.
Answer: Option c: $1$.
Key concepts and techniques used: Key pattern identification -- Use of basic algebraic simplifying relation, $(a+b)(a-b)=a^2-b^2$ -- Use of basic trigonometric relation $(\sin^2 \theta+\cos^2 \theta)=1$ -- Solving in mind.
All the processing could easily be done mind.
Problem 4.
The value of $\displaystyle\frac{1}{\sin^4(90^0-\theta)}+\displaystyle\frac{1}{\cos^2(90^0-\theta)-1}$ is,
- $\tan^4 \theta$
- $\tan^2 \theta\sec^2 \theta$
- $\sec^4 \theta$
- $\tan^2 \theta\sin^2 \theta$
Solution 4. Problem analysis: First convert complementary angles and then simplify
Converting complementary angles first, we get the target expression $E$ as,
$E=\displaystyle\frac{1}{\sin^4(90^0-\theta)}+\displaystyle\frac{1}{\cos^2(90^0-\theta)-1}$
$=\displaystyle\frac{1}{\cos^4 \theta}+\displaystyle\frac{1}{\sin^2 \theta-1}$.
Then it is straightforward trigonometric simplification,
$E=\displaystyle\frac{1}{\cos^4 \theta}-\displaystyle\frac{1}{\cos^2 \theta}$, coverting $1-\sin^2 \theta$ to $\cos^2 \theta$,
$=\displaystyle\frac{1}{\cos^2 \theta}(\sec^2 \theta-1)$
$=\tan^2 \theta\sec^2 \theta$.
Answer: Option b: $\tan^2 \theta\sec^2 \theta$.
Key concepts and techniques used: Complentary angle functions -- Basic trigonometry concepts -- Solving in mind.
Problem 5.
The value of $\sin(B-C)\cos(A-D)$
$\hspace{22mm}+\sin(A-B)\cos(C-D)$
$\hspace{22mm}+\sin(C-A)\cos(B-D)$ is,
- $\displaystyle\frac{3}{2}$
- $0$
- $-3$
- $1$
Solution 5. Problem analysis and Solution by mathematical reasoning
Each of the three product terms will expand to 4 unique terms because of the unique angle and function distribution. No term will be cancelled out within each product result and after expansion then, total number of terms will be 12.
The important pattern in these 12 terms identified is—each of the 12 terms consists of four unique factors of $\sin$ and $\cos$ using all the four angles.
Continuing our deductive reasoning it is obvious then,
All these 12 compound terms (each with four factors in $\sin$ and $\cos$) must cancel out against each other to generate the final result free of any variable.
Finally we reason that—if six of these twelve terms cancel out against the other six, the final result can only be 0, not any non-zero integer.
You may actually expand and be convinced that our reasoning is indeed true.
Answer: Option b: $0$.
Key concepts and techniques used: Problem analysis -- Key pattern identification -- Deductive reasoning -- Mathematical reasoning -- Solving in mind.
Problem 6.
The value of $\left[\tan^2(90^0-\theta)-\sin^2(90^0-\theta)\right]$
$\hspace{22mm}\times{\text{cosec}^2(90^0-\theta)\text{cot}^2(90^0-\theta)}$ is,
- $1$
- $0$
- $2$
- $-1$
Solution 6. Problem analysis and complementary angle conversion to elementary angles
At the first stage we convert all the complementary angle functions to elementary angle functions,
$\left[\tan^2(90^0-\theta)-\sin^2(90^0-\theta)\right]$
$\hspace{22mm}\times{\text{cosec}^2(90^0-\theta)\text{cot}^2(90^0-\theta)}$
$=(\text{cot}^2 \theta-\cos^2 \theta)\sec^2 \theta\tan^2 \theta$
$=(\sec^2 \theta-\tan^2 \theta)$
$=1$.
After complementary angle function conversion, it is straightforward trigonometric simplification.
Answer: Option a: 1.
Quick and all in mind.
Key concepts and techniques used: Basic trigonometry copncepts -- Complementary angle trigonometric functions -- friendly trigonometric function pairs.
Problem 7.
The value of $\displaystyle\frac{4}{3}\text{cot}^2\left(\displaystyle\frac{\pi}{6}\right)+3\cos^2(150^0)$
$\hspace{22mm}-4\text{cosec}^245^0+8\sin\left(\displaystyle\frac{\pi}{2}\right)$ is,
- $1$
- $\displaystyle\frac{13}{2}$
- $-\displaystyle\frac{7}{2}$
- $\displaystyle\frac{25}{4}$
Solution 7. Problem analysis and conversion to angles in degrees using supplementary angle function
The angle in the first term evaluates to $30^0$ and the fourth term, $90^0$. But the second term involves supplementary angle function,
$\cos^2(150^0)=\cos^2(90^0+60^0)=\sin^2 60^0=\displaystyle\frac{3}{2}$.
Substituting the trigonometric ratio values the target expression becomes,
$E=\displaystyle\frac{4}{3}\text{cot}^2\left(\displaystyle\frac{\pi}{6}\right)+3\cos^2(150^0)$
$\hspace{22mm}-4\text{cosec}^245^0+8\sin\left(\displaystyle\frac{\pi}{2}\right)$
$=\displaystyle\frac{4}{3}\times{\displaystyle\frac{\displaystyle\frac{3}{4}}{\displaystyle\frac{1}{4}}}+3\times{\displaystyle\frac{3}{4}}-4\times{2}+8$
$=4+\displaystyle\frac{9}{4}$
$=\displaystyle\frac{25}{4}$.
Answer: Option d: $\displaystyle\frac{25}{4}$.
Key concepts and techniques used: Supplementary angle functions -- Trigonometric ratio values -- Basic trigonometry concepts.
Problem 8.
The value of $\displaystyle\frac{\tan 5\theta+\tan 3\theta}{4\cos 4\theta(\tan 5\theta-\tan 3\theta)}$ is,
- $\tan 4\theta$
- $\sin 2\theta$
- $\cos 2\theta$
- $\text{cot }2\theta$
Solution 8. Problem solving using compound angle and multiple angle trigonometric relations
Given expression,
$\displaystyle\frac{\tan 5\theta+\tan 3\theta}{4\cos 4\theta(\tan 5\theta-\tan 3\theta)}$
$=\displaystyle\frac{\sin 5\theta\cos 3\theta+\cos 5\theta\sin 3\theta}{4\cos 4\theta(\sin 5\theta\cos 3\theta-\cos 5\theta\sin 3\theta)}$, as inverse of $\cos 5\theta\cos 3\theta$ cancel out between numerator and denominator,
$=\displaystyle\frac{\sin 8\theta}{4\cos 4\theta\sin 2\theta}$, as $\sin (5\theta+3\theta)=\sin 8\theta$ and $\sin (5\theta-2\theta)=\sin 2\theta$,
$=\displaystyle\frac{2\sin 4\theta\cos 4\theta}{4\cos 4\theta\sin 2\theta}$
$=\displaystyle\frac{4\sin 2\theta\cos 2\theta}{4\sin 2\theta}$
$=\cos 2\theta$.
Answer: Option c: $\cos 2\theta$.
Key concepts and techniques used: Basic trigonometry concepts -- Compound angle concepts -- Multiple angle concepts.
Though the steps seem to be many, deduction was simple enough to reach the solution quickly.
Problem 9.
The value of $\displaystyle\frac{\sin(y-z)+\sin(y+z)+2\sin y}{\sin(x-z)+\sin(x-z)+2\sin x}$ is,
- $\cos x\sin y$
- $\sin x\tan y$
- $\sin z$
- $\displaystyle\frac{\sin y}{\sin x}$
Solution 9. Problem analysis and strategy decision
Each pair of compound angle $\sin$ functions in the numerator and denominator when expanded will have two terms cancelled out leaving twice of the other term. At the next stage the third term can be taken out as a factor so that the other factor will cancel out between numerator and denominator. Final result will then be, $\displaystyle\frac{\sin y}{\sin x}$.
Let us show you the deductions.
Solution 9. Deductive steps
Given expression,
$\displaystyle\frac{\sin(y-z)+\sin(y+z)+2\sin y}{\sin(x-z)+\sin(x-z)+2\sin x}$
$=\displaystyle\frac{2\sin y\cos z+2\sin y}{2\sin x\cos z+2\sin x}$
$=\displaystyle\frac{2\sin y(1+\cos z)}{2\sin x(1+\cos z)}$
$=\displaystyle\frac{\sin y}{\sin x}$.
Answer: Option d: $\displaystyle\frac{\sin y}{\sin x}$.
Key concepts and techniques used: Compound angle trigonometric functions -- Solving in mind.
All in mind and in quick time.
Problem 10.
The value of $\displaystyle\frac{\sin(90^0-10\theta)-\cos(\pi-6\theta)}{\cos\left(\displaystyle\frac{\pi}{2}-10\theta\right)-\sin(\pi-6\theta)}$ is,
- $\cos \theta$
- $\tan 2\theta$
- $\text{cot }3\theta$
- $\text{cot }2\theta$
Solution 10. Problem analysis: Conversion of complementary and supplementary angle trigonometric function relations at Stage 1
The compound angle relations we'll use here are,
$\sin(90^0-\alpha)=\cos \alpha$, a complementary angle relation,
$\cos(90^0-\alpha)=\sin \alpha$, a complementary angle relation,
$\sin(\pi-\alpha)=\sin \alpha$, a supplementary angle relation,
$\cos(\pi-\alpha)=-\cos \alpha$, a supplementary angle relation.
Applying these relations, the given expression gets simplified to,
$E=\displaystyle\frac{\sin(90^0-10\theta)-\cos(\pi-6\theta)}{\cos\left(\displaystyle\frac{\pi}{2}-10\theta\right)-\sin(\pi-6\theta)}$
$\hspace{5mm}=\displaystyle\frac{\cos 10\theta+\cos 6\theta}{\sin 10\theta-\sin 6\theta}$.
Solution 10. Applying submultiple of compound angle relations with angles $\left(\displaystyle\frac{A+B}{2}\right)$ and $\left(\displaystyle\frac{A-B}{2}\right)$ at Stage 2
The derived relations on submultiple of compound angles generally used are,
$\sin A+\sin B=2\sin\left(\displaystyle\frac{A+B}{2}\right)\cos\left(\displaystyle\frac{A-B}{2}\right)$,
$\sin A-\sin B=2\cos\left(\displaystyle\frac{A+B}{2}\right)\sin\left(\displaystyle\frac{A-B}{2}\right)$,
$\cos A +\cos B=2\cos\left(\displaystyle\frac{A+B}{2}\right)\cos\left(\displaystyle\frac{A-B}{2}\right)$, and
$\cos A -cos B=2\sin\left(\displaystyle\frac{A+B}{2}\right)\sin\left(\displaystyle\frac{A-B}{2}\right)$
We will repeat the mechanism of the first relation below. The other three can be derived in the same way. If you already know this concept, you may skip it.
Rich trigonometric relation on submultiple of compound angles
The mechanism behind $\sin A+\sin B=2\sin\left(\displaystyle\frac{A+B}{2}\right)\cos\left(\displaystyle\frac{A-B}{2}\right)$
Assuming $\displaystyle\frac{A+B}{2}=\alpha$ and $\displaystyle\frac{A-B}{2}=\beta$, we get,
$(\alpha+\beta)=A$, and
$(\alpha-\beta)=B$.
So,
$\sin(\alpha+\beta)+\sin(\alpha-\beta)=2\sin \alpha\cos \beta$,
Or, $\sin A+\sin B=2\sin \left(\displaystyle\frac{A+B}{2}\right)\cos \left(\displaystyle\frac{A-B}{2}\right)$.
Taking the problem solving thread again, we have,
$E=\displaystyle\frac{\cos 10\theta+\cos 6\theta}{\sin 10\theta-\sin 6\theta}$
$=\displaystyle\frac{2\cos 8\theta\cos 2\theta}{2\cos 8\theta\sin 2\theta}$
$=\text{cot }2\theta$.
Answer: Option d: $\text{cot }2\theta$.
Key concepts and techniques used: Complementary angle trigonometric functions -- Supplementary angle trigonometric functions -- Compound angle trigonometric functions -- Submultiple of compound angle trigonometric relations -- Multiple angle trigonometric relations.
Guided help on Trigonometry in Suresolv
To get the best results out of the extensive range of articles of tutorials, questions and solutions on Trigonometry in Suresolv, follow the guide,
The guide list of articles is up-to-date.
